길 찾기 알고리즘

 Dijkstra는 대표적인 길찾기 알고리즘입니다.

Dijkstra 알고리즘을 이용하여 출발 노드에서 종말 노드로 가는 최단 거리(최소 비용)의 경로를 찾을 수 있습니다.

아래와 같은 그래프를 생각해봅시다.

그래프

B에서 출발해 E에 도착하는 경로는 여러개가 있습니다.

여러개의 경로 중에서 최소 비용을 가지는 경로가 우리가 원하는 경로가 될것입니다.

노드에서 노드 사이를 옮겨다닐때 비용이 발생한다고 하면

경로의 비용은 $Cost(path) = \sum\limits_{i=1}^n Cost(edge),\text{ }(edge_1,edge_2...edge_n은\text{ }path에\text{ }속함)$이 됩니다.

$edge$가 노드와 노드를 연결하니 $edge$에 비용을 추가하면 아래와 같이 됩니다.

cost 추가

그럼 이제 경로를 구성하는 $edge$를 구하면 됩니다.

방문한 노드들을 트리 형식으로 구축하여 경로를 구성하는 $edge$들을 구할 수 있습니다.

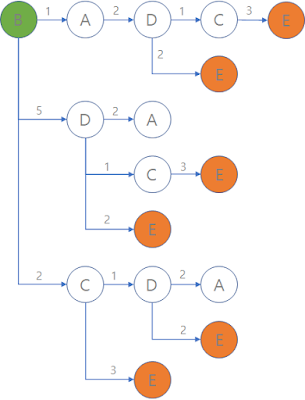B-E 경로들

B에서 출발해 E에 도달하는 총 6개의 경로를 구할 수 있습니다.
(주의: 진행 중인 경로에 속한 노드를 재방문할 수 없습니다. 그렇지 않으면 무한루프에 빠지게 됩니다.)

경로들에 대한 비용을 계산해 보면,

$\begin{eqnarray} B\to A\to D\to C\to E &= 9 \\ B\to A\to D\to E  &= 6 \\ B\to D\to C\to E &= 10 \\ B\to D\to E &= 7 \\ B\to C\to D\to E &= 5 \\ B\to C\to E &= 6 \end{eqnarray}$

$B\to C \to D \to E$가 최소 비용 거리임을 확인 할 수 있습니다.

최소 비용 거리

$Cost(edge)$를 거리로 두면 최단 거리, 시간으로 두면 최소 시간의 경로를 구할 수 있습니다.

그래서 제가 앞에서 최단 거리와 최소 비용를 혼용한 이유이기도 합니다.

$Cost(edge)$ 함수를 다항식으로 두면 다양한 조건들을 반영할 수 있는 비용 함수를 만들 수 있습니다.
예를 들면 아래 비용 함수는 거리과 edge의 방향이 바뀌었을때의 비용 함수입니다.

$$Cost(edge)=length + turning\text{ }point$$
이 비용 함수를 이용해서 $edge$의 방향이 최소로 바뀌는 경로를 구할 수 있습니다.

여기서 추가적으로 자동차 내비게이션처럼 경유 경로를 적용하는 것에 대해 알아 봅시다.
위의 예에서 A를 경유해서 지나가야 한다면 

$$ min(B\to E) = min(B\to A) + min(A\to E) $$($B\to A$의 최소 비용 경로와 $A\to E$의 최소 비용 경로는 같은 노드를 공유하지 않음)
로 표현할 수 있습니다.

B에서 출발하여 A에 도착하는 최소 비용 경로와 A에서 출발하여 E에 도착하는 최소 비용 경로를 합하면 B에서 출발하여 E에 도착하는 최소 비용 경로와 같습니다.

과연 그럴까요? 확인해봅시다.

$B\to A$의 두 경로 ${B\to A}, {(B\to A)}^{'} $가 있으면 $B\to E$의 비용은 아래와 같이 표현됩니다.
$$ \begin{eqnarray} \begin{aligned} Cost(B\to E) &= Cost(B\to A) + Cost(A\to E) \\ &= Cost({(B\to A)}^{'}) + Cost(A\to E) \end{aligned} \end{eqnarray} $$

두 식에서 두번째 항의 최소 비용은 동일하기 때문에 전체 식에서 최소 비용이 되기 위해서는 첫번째 항이 최소 비용이 되어야 합니다.
따라서 $B\to A$의 최소 비용과 $A\to E$의 최소 비용의 합이 전체 경로의 최소 비용이 됩니다.

마지막으로 $A$를 회피해서 가야한다면 어떻게 하면 될까요?

간단하게 $A$로 접근 가능한 $edge$를 비활성화 시키면 됩니다.

$A$에 도달할 수 있는 $edge$가 없기 때문에 $A$를 회피하게 됩니다.